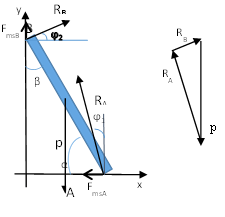
Thanh dựng nghiêng:

Dựng thanh dài có trọng lượng P vào tường thẳng đứng, hệ số ma sát giữa sàn và thanh là μ₁; góc nghiêng giữa thanh và sàn là α; Xác định α_min để thanh còn đứng yên. Xét các trường hợp:

1. Tường nhẵn: μ₂ = 0;
2. Sàn nhẵn: μ₁ = 0;
3. μ₁ = μ₂ = 0;
4. Tường, sàn và thanh đều bằng gỗ (μ₁ = μ₂ = 0,4).

Giải: Vẽ hệ tọa độ Oxy; Oy là tường, Ox là sàn;

Điểm B là điểm đầu thanh tiếp xúc tường (dựa vào tường) => F_msB hướng lên, điểm A là điểm đầu thanh tiếp xúc sàn => F_msA nằm ngang hướng sang trái (thanh trượt sang phải), φ1 là góc nghiêng của R_A so với phương thẳng đứng, φ2 là góc nghiêng của R_B so với phương nằm ngang.

Giải:  Gọi góc ma sát với tường là φ₂ với tan φ₂ = μ₂; Gọi góc ma sát với sàn là φ₁ với tan φ₁ = μ₁;

R_A = F_msA + N_A ; (in đậm là vec tơ) N_A song song cùng chiều với Oy, N_B song song cùng chiều với Ox;

R_B = F_msB + N_B; với

N_A = R_A cos φ₁; N_B = R_B cos φ₂ ;

Có 3 lực tác dụng vào thanh là p , R_A và R_B . Để  thanh cân bằng thì R_A + R_B + p = 0      (*)

(tam giác lực khép kín);

Chiếu phương trình (*) lên Ox và Oy ta có:

N_B – F_msA = 0 ;                                                         (1)

– p + N_A + F_msB = 0 => F_msB = p – N_A ;             (2) (F_msB ≈ 0 vì nó không quan trọng khi thanh trượt)

Ta có: tan φ₁ = N_B/N_A  ≈ N_B /p = F_msA / p  (xem (1)) => F_msA = p tan φ₁ ;

Xét trong phạm vi từ 0⁰ đến 90⁰, từ hình vẽ ta có: tan α  ≤  (p / F_msA)

⇔ tan α ≤ p/(p tan φ1) ⇔ tan α ≤ (1/ tan φ₁) ⇔ α ≥ 90⁰ – φ₁                                 (3)

=> α_min = 90⁰ – φ₁ với φ₁ = arctan μ₁; Khi α_min thì R_A dọc theo thanh => R_B = N_B => F_msB = 0

=> Ma sát với tường không quan trọng, (tường nhẵn vẫn được, thường bỏ qua ma sát với tường)

1. Từ (3) => α_min = 90⁰ – φ₁ ;
2. φ₁ = 0; Từ (3) => α_min = 90⁰: Thanh đứng thẳng song song với tường.
3. Thanh đặt nằm.
4. Từ (3) => α_min = 68,2⁰.