- Liên hệ trung tâm
- 090 6800 598
- [email protected]
Con lắc lò xo: Thế năng điều hòa
Con lắc lò xo: Thế năng điều hòa
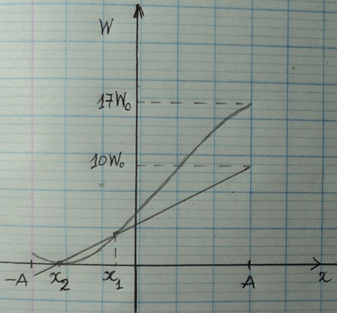
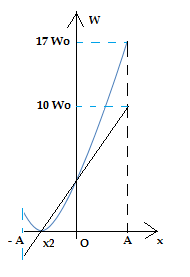
Con lắc lò xo: Thế năng điều hòa: Một con lắc lò xo dao động điều hòa theo phương thẳng đứng dọc theo trục Ox, chiều dương hướng xuống, gốc O tại vị trí cân bằng của vật. Chọn gốc thế năng điều hòa tại O, hình vẽ biểu diễn sự phụ thuộc của thế năng trọng trường và thế năng đàn hồi vào ly độ x của dao động, trong đó x1 – x2 = 2,66 cm. Biên độ dao động của con lắc lò xo gần nhất với giá trị nào sau đây:
A. 8 cm; B. 7 cm; C. 6 cm; D. 5 cm.
Giải: Gọi D là đầu tự do của lò xo khi chưa treo vật, Với D là gốc thế năng, ta có:
Tại x = A: Thế năng trọng trường là: Wp = mg(A + ∆l0) = 10 W0; (đường thẳng là đồ thị Wp);
Thế năng đàn hồi là: Wđh = |- ½ k(A + ∆l0)2| = 17 W0;
Vậy thế năng điều hòa của con lắc tại x = A là:
Wt (x=A) = (1/2)kx2 = Wđh+ Wp = – ½ k(A + ∆l0)2 + 10W0 = (-17 + 10) W0 = -7 W0 (xét công tổng hợp nên phải xét dấu của công và công của lực đàn hồi lúc này là công âm và có độ lớn, lớn hơn công của trọng lực)
Vì Wt (x=A) là hiệu của hai thế năng nên không phụ thuộc vào gốc thế năng là D hay O;
Mặt khác ta có: Với gốc thế năng tại vị trí cân bằng O, thì thế năng điều hòa của con lắc là:
Wt (x=A) = (1/2)kx2 = ½ kA2 = 7 W0; (1) (xem trên)
và ½ k(A + ∆l0)2 = 17 W0; (từ đồ thị Wđh) (2)
Lập tỷ (2) và (1) ta có: (A + ∆l0)/A = √(17/7) => ∆l0/A = 0,56; (3)
Từ đồ thị ta thấy, tại x2 lò xo không biến dạng, khi lò xo giãn đến x1 (vật đi xuống từ x2 đến x1), thì độ biến dạng của lò xo hay độ dời của vật là 2,66 cm, tại x1 có Wđh = Wp => x1 là vị trí cân bằng O, vậy ta có:
=> ∆l0 = 2,66 cm;
Từ (3) => A = 4,75 cm. Chọn D. Hình vẽ lại: