- Liên hệ trung tâm
- 090 6800 598
- [email protected]
Sóng ngang – Đồ thị
Sóng ngang – Đồ thị
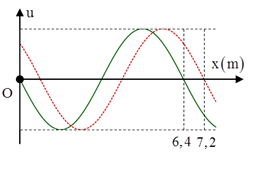
Cho một sợi dây cao su căng ngang, làm cho đầu O của dây dao động theo phương thẳng đứng. Hình vẽ mô tả hình dạng sợi dây tại thời điểm t1 (đường nét liền) và tại thời điểm t2 = t1 + 0,2 s; Tại thời điểm t3 = t2 + 0,6 s thì độ lớn li độ của phần tử M cách đầu dây một đoạn 2,4 m (tính theo phương truyền sóng) là √3 cm. Gọi δ là tỉ số của tốc độ cực đại của phần tử trên dây với tốc độ truyền sóng. Giá trị của δ gần giá trị nào nhất sau đây?
A. 0,025; B. 0,018; C. 0,012; D. 0,022
Giải: + Từ đồ thị ta có λ = 6,4 m;
Vận tốc truyền sóng v = (7,2 – 6,4)/0,2 s = 4 m/s;
Tần số dao động của các phần tử: ω = 2π / T = 2πv / λ = 5π/4 rad/s => T = 8/5 = 1,6 s;
+ Độ lệch pha giữa M và O: ∆φ = 2πxM/λ = 2π. 2,4/6,4 = 3π/4 rad;
Ta có: t3 – t1 = 0,8 s = T/2 ; 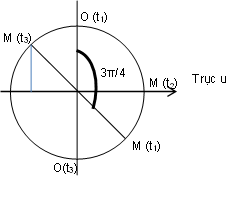
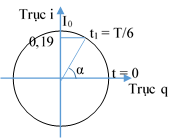
Từ đồ thị ta vẽ được vị trí của O và M tại các thời điểm trên vòng tròn lượng giác, từ đó ta thấy
uM(t3) = |- A cos(450)| = √3 cm => A = √6 cm
=> Tốc độ cực đại của phần tử trên dây là : vmax = Aω = 5π√6 /4 = 9,62 cm/s = 0,0962 m/s
=> δ = 0,0962/4 = 0,024. Chọn D.