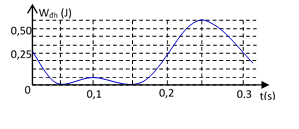
*** Một con lắc lò xo treo vào một điểm cố định ở nơi có gia tốc trọng trường g = π² (m/s²). Cho con lắc dao động  điều hòa theo phương thẳng đứng, Hình trên là đồ thị biểu diễn sự phụ thuộc của thế năng đàn hồi W_đh của lò xo vào thời gian t. Khối lượng của con lắc gần nhất với giá trị nào sau đây?

A. 0,65 kg.          B. 0,35 kg.              C. 0,55 kg.       D. 0,45 kg.

Giải: Lò xo treo thẳng đứng (hình vẽ)

Lưu ý: Gốc thế năng đàn hồi, tại vị trí lò xo có chiều dài tự nhiên.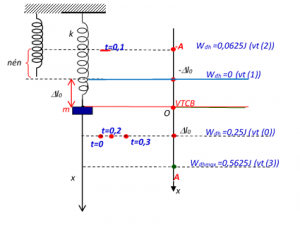

Theo đồ thị, mỗi đoạn có thế năng: 0,25 /4 = 0,0625 J.

Tại vị trí (2) vật lên cao nhất (x = – A) thế năng đàn hồi:

W(2) = 0,0625 = ½ k(A – Δl₀)²              (1*)

Tại vị trí (3) vật xuống thấp nhất (x = A) thế năng đàn hồi cực đại:

W(3) = 0,5625 = ½ k(A + Δl₀)²              (2*)

Lấy (2*) chia (1*), sau khi biến đổi và rút gọn ta có: A = 2 Δl₀                (3*)

Khi t = 0, vật ở vị trí (0): x = x₀, thế năng đàn hồi:

W(0) = 0,25 = ½ k(x₀ + Δl₀)²                 (4*)

Lập tỷ (2*) và (4*) vế theo vế, kết hợp với (3*) ta tính được x₀ = A/2 = Δl₀.

Mô tả: Khi t = 0, vật bắt đầu đi lên từ vị trí (0), đến khi t = 0,05 s vật ở vị trí (1), đến khi t = 0,1 s vật ở vị trí (2), rồi đi xuống tới vị trí (1) lúc t = 0,15 s, rồi đi xuống tiếp tới vị trí (0) lúc t = 0,2 s, rồi đi tiếp tới vị trí (3) lúc t = 0,25 s; tiếp theo đi lên tới vị trí (0) lúc t = 0,3 s là hoàn thành một chu kỳ dao động => T = 0,3 s;

Mặt khác ta biết con lắc lò xo treo có chu kì: T = 2π√(m/k) = 2π √ (Δl₀ /g) => Δl₀ = T²g / (4π²) = 0,09/4 m = 2,25 cm => A = 4,5 cm thay vào (1*) ta được k = 247 N/m => m = T²k / (4π²) = 0,56 kg . Chọn C.