- Liên hệ trung tâm
- 090 6800 598
- [email protected]
Hai con lắc đơn – Gặp nhau – Cùng ly độ
Hai con lắc đơn – Gặp nhau – Cùng ly độ
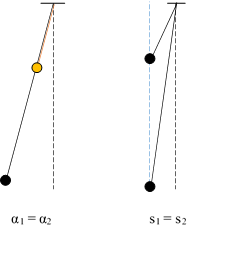
Hai con lắc đơn có khối lượng như nhau, cùng dao động điều hòa với biên độ nhỏ trong hai mặt phẳng thẳng đứng song song nhau. Biết chu kì con lắc thứ nhất gấp 2 lần chu kì con lắc thứ hai, biên độ của con lắc thứ hai gấp 3 lần biên độ của con lắc thứ nhất. Chọn mốc thế năng của mỗi con lắc ở vị trí cân bằng của chúng. Tại một thời điểm nào đó, hai con lắc có cùng li độ, đồng thời động năng con lắc thứ nhất gấp 3 lần thế năng của nó. Tỉ số giữa tốc độ của con lắc thứ hai và con lắc thứ nhất tại thời điểm đó bằng
A. 144/3; B. 140/3; C. √(140/3); D. √(144/3).
Giải: T1 = 2T2 => l1 = 4l2 ; s02 = 3s01 <=> l2α02 = 3l1α01 => α02 = 12α01 ;
Vị trí mà động năng con lắc thứ nhất gấp ba lần thế năng của nó là: α1 = α01 /2 ;
Vì chiều dài hai con lắc khác nhau, nên khi hai con lắc gặp nhau, lúc đó ly độ góc của hai con lắc :
α2 = α1 = α01 /2 = α02 /24 ;
Ta biết tốc độ của con lắc đơn là
v2 = 2gl (cosα – cosα0) ≈ 2gl [(½ sin2α0) – (½ sin2α)] ≈ gl (α02 – α2) ;
Tốc độ của các con lắc là:
v12 = gl1 (α012 – α12) = gl1. ¾ . α012 = 3gl2 α012 ; (1)
v22 = gl2 (α022 – α22) = gl2 [(242 – 1) /4] α022 = gl2 [575 /4] α012 = 143,75 gl2 α012 ; (2)
Từ (1) và (2) ta có v2 / v1 = √(143,75 /3) = 6,92 => Chọn D.
Giải: T1 = 2T2 => l1 = 4l2 ; s02 = 3s01 và ω2 = 2ω1 ;
Vị trí mà động năng con lắc thứ nhất gấp ba lần thế năng của nó là: α1 = α01 /2 hay s1 = s01 /2 ;
Khi hai con lắc có cùng ly độ : s1 = s2 = s02 /6 ;
Ta có: v = ω√(s02 – s2); Vậy: v2 = ω2√(s022 – s22) = ω2√[s022 – (s022/36)] = ω2√(35s022 /36) ; (1)
v1 = ω1√(s012 – s12) = 0,5 ω2√[(s022 /9) – (s022 /36)] = 0,5 ω2√(s022 /12) ; (2)
Từ (1) và (2) ta có v2 / v1 = 2√(35 /3) = √(140/3) = 6,83 => Chọn C.