- Liên hệ trung tâm
- 090 6800 598
- [email protected]
2021-TNQG-lần 2-câu 40 mã đề 209 – Giao thoa cơ
2021-TNQG-lần 2-câu 40 mã đề 209 – Giao thoa cơ
Giao thoa sóng cơ – Thi TNQG 2021 lần 2 ngày 7 / 8 / 2021 – Mã đề 209
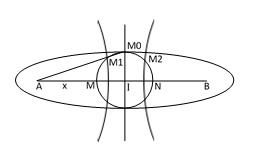
Câu 40. Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại A và B, dao động cùng pha theo phương thẳng đứng, phát ra hai sóng lan truyền trên mặt nước với bước sóng λ . Trên đoạn thẳng AB có n điểm cực tiểu giao thoa, trong đó M và N là hai điểm cực tiểu giao thoa đối xứng qua trung điểm của AB (MA < NA). Trên mặt nước, (C) là đường tròn đường kính MN. Trong các điểm cực đại giao thoa trên (C) có 6 điểm mà phân tử nước tại đó dao động cùng pha với hai nguồn. Biết 13 < n < 17. Độ dài đọan thẳng AM có giá trị gần nhất với giá trị nào sau đây?
A. 0,6λ. B. 1,5λ. C. 1,1λ. D. 0,2λ.
Giải:
Gọi I là trung điểm của AB; đặt AB = 2d λ ; (Chọn đơn vị là λ);
13 < n < 17 => n = 14 hoặc 16 => bậc cực đại giao thoa trên AB là: kmax = 7 hoặc 8 ; (1)
N là cực tiểu giao thoa thứ (kN + 1) với kN = 2, 3, …, 5, 6 ; Trên hình M1 ; M0 ; và M2 là 3 điểm mà phân tử nước tại đó dao động cùng pha với hai nguồn và là cực đại giao thoa => trên (C) có đủ 6 điểm cực đại giao thoa mà phân tử nước tại đó dao động cùng pha với hai nguồn ; (Hai đường hypecbol qua M1 và M2 đối xứng nhau qua đường IM0). Đề cho M là cực tiểu giao thoa nên IM = IN = IM0 = R = (kNλ/2) + (λ/4) = (0,5kN + 0,25) λ ;
Trong các bài trước ta đã chứng minh được M0 là điểm mà phân tử nước tại đó dao động cùng pha với hai nguồn thì AM0 + BM0 = 2mλ với m là số nguyên => M0 thuộc ellip như hình vẽ , ellip này có
Trục lớn 2a = 2mλ ; 2c = AB = 2dλ và
Trục nhỏ b = √(a2 – c2) = R = [√(m2 – d2)]λ = (0,5kN + 0,25)λ => d = √[m2 – (0,5kN + 0,25)2] λ;
Ta có AM = dλ – R = x = {√[m2 – (0,5kN + 0,25)2] – (0,5kN + 0,25)} λ (2)
Dùng Shift solve giải phương trình (2) với x là giá trị ở mỗi đáp án, với mỗi giá trị x tham số kN lần lượt nhận giá trị 6; 5; …; 3; 2; giải (2) để tìm m nguyên, kết quả như sau:
| Đáp án của đề | k = kN | m | Kết quả m, k thay vào (2) tính lại x |
| A. x = 0,6 | 6 | 5,03835 | m = 5 ; k = 6 => x = 0,55 ≈ 0,6 (3) |
| 5 | 4,33417 | ||
| 4 | 3,63110 | ||
| 3 | 2,93002 | ||
| 2 | 2,23270 | ||
| B. x = 1,5 | 6 | 5,75343 | |
| 5 | 5,06211 | m = 5 ; k = 5 => x = 1,43 ≈ 1,5 (4) | |
| 4 | 4,37321 | ||
| 3 | 3,69121 | ||
| 2 | 3,02076 | m = 3 ; k = 2 => x = 1,48 ≈ 1,5 (5) | |
| C. x = 1,1 | 6 | 5,43000 | |
| 5 | 4,73128 | ||
| 4 | 4,03547 | m = 4 ; k = 4 => x = 1,06 ≈ 1,1 (6) | |
| 3 | 3,34439 | ||
| 2 | 2,66177 | ||
| D. x = 0,2 | 6 | 4,73973 | |
| 5 | 4,03299 | m = 4 ; k = 5 => x = 0,15 ≈ 0,2 (7) | |
| 4 | 3,32641 | ||
| 3 | 2,62011 | ||
| 2 | 1,91441 |
(Nhận xét: Kết quả (3); (5) và (7): m và k không phải cùng là số lẻ, hoặc cùng là số chẵn, vẫn có cực đại giao thoa cùng pha với nguồn)
Thử lại các kết quả:
Với (3) => R = 3,25 λ => AB = 2d λ= 2 (0,55 + 3,25) λ = 7,6 λ => Số cực đại trên AB là 15 => n = 14 thoả đề bài; sai số so với đáp án A là 8,39 %.
Với (4) => R = 2,75 λ => AB = 2d λ= 2 (1,43 + 2,75) λ = 8,4 λ => Số cực đại trên AB là 17 => n = 16 thoả đề bài; sai số so với đáp án B là 4,60 %.
Với (5) => R = 1,25 λ => AB = 2d λ= 2 (1,48 + 1,25) λ = 5,5 λ => Số cực đại trên AB là 11 => n = 10 không thoả đề bài : Loại.
Với (6) => R = 2,25 λ => AB = 2d λ= 2 (1,06 + 2,25) λ = 6,62 λ => Số cực đại trên AB là 13 => n = 12 không thoả đề bài : Loại.
Với (7) => R = 2,75 λ => AB = 2d λ= 2 (0,15 + 2,75) λ = 5,8 λ => Số cực đại trên AB là 11 => n = 10 không thoả đề bài : Loại.
Trong hai kết quả (3) và (4) ta chọn (4) đáp án B: x = 1,5 λ vì có sai số nhỏ hơn. Chọn B.