DAO ĐỘNG ĐIỀU HOÀ – THI THPT QG 2022

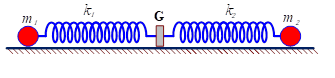
Câu 37 mã đề 221 thi THPT QG 2022: Hình bên mô tả một hệ gồm hai con lắc lò xo nằm ngang, đồng trục cùng được gắn vào giá G. Các lò xo nhẹ k₁ và k₂ có độ cứng lần lượt là 32 N/m và 12 N/m. Các vật nhỏ m₁ và m₂ có khối lượng lần lượt là 512 g và 192 g. Đưa hai vật đến các vị trí sao cho cả hai lò xo cùng dãn 15 cm rồi thả nhẹ m₁ để m₁ dao động điều hòa. Sau khi thả m₁ mộ̣t khoảng thời gian Δt thì thả nhẹ m₂ để m₂ dao động điều hòa. Biết rằng G được gắn với sàn, G không bị trượt trên sàn khi hợp lực của các lực đàn hồi cùa hai lò xo tác dụng vào G có độ lớn không vượt quá 4,2 N. Lấy π² = 10. Giá trị lớn nhất của Δt để G không bao giờ bị trượt trên sàn là

A. 2/ 15 s.                            B. 4/15 s.                                   C. 1/3 s.                             D. 1/15 s.

Giải: Chọn gốc thời gian là lúc thả nhẹ vật m₂

F_đh1 = -k₁x₁ = -32. 0,15 cos (2,5πt + (2,5π.Δt)) (N) với w₁ = w₂ = 2,5π rad/s.

= 4,8 cos (2,5πt + (2,5π.Δt) – π) (N)

F_đh2 = -k₂x₂ = -12. 0,15 cos (2,5πt) (N) với w₁ = w₂ = 2,5π rad/s.

= 1,8 cos (2,5πt – π) (N)

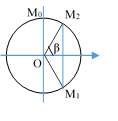
Tổng hợp lực đàn hồi tác dụng lên G là: Vì chiều dương của 2 con lắc ngược nhau nên F_đh = F_đh1 – F_đh2 = 4,2 cos (2,5πt + φ) N;

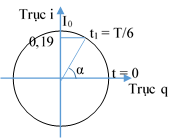
Ta có giản đồ vector như hình vẽ, F_đh lớn nhất khi nó nằm ngang ứng với góc quay α +β

=> Độ lệch pha giữa F_đh1 và F_đh2 là: Δφ = w. Δt = 2,5π. Δt (rad) = α  ;

Áp dụng hệ thức lượng trong tam giác ta có:

4,2² = 4,8² + 1,8² – (2. 1,8. 4,8 cosα) => cosα = 1,2 => α = π/3 rad;

1,8² = 4,2² + 4,8² – (2. 4,2. 4,8 cosβ) => cosβ = 13/14 => β = 0,38025 rad ;

=> Δφ = α => Δt = T/6 = 2/15 s . Chọn A.