- Liên hệ trung tâm
- 090 6800 598
- [email protected]
GT M ngoài đường tròn cùng pha với nguồn
GT M ngoài đường tròn cùng pha với nguồn
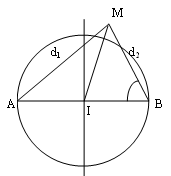
Ở mặt chất lỏng, tại hai điểm A và B có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp có bước sóng λ . Gọi I là trung điểm của đoạn thẳng AB = 6,6λ. Ở mặt chất lỏng, gọi (C) là hình tròn nhận AB là đường kính, M là một điểm ở ngoài (C) gần I nhất mà phần tử chất lỏng ở đó dao động với biên độ cực đại và cùng pha với nguồn. Độ dài đoạn thẳng MI có giá trị gần nhất với giá trị nào sau đây?
A. 3,41λ; B. 3,76λ; C. 3,31λ; D. 3,54λ;
Giải: Ta có số cực đại giao thoa trên AB thỏa: – 6,6 < k < 6,6 => kmax = 6;
M là cực đại giao thoa nên d1 – d2 = kλ; với k = 0; ±1; ±2; .. ±6;
M cùng pha với nguồn nên d1 + d2 = 2mλ; với m là số nguyên; từ 2 phương trình trên ta được :
d1 = m + 0,5k; d2 = m – 0,5k; với λ là đơn vị; (1)
Hệ thức lượng trong tam giác cho:
d12 = d22 + AB2 – (2 d2ABcosB) => cosB = (d22 + AB2 – d12) / (2AB.d2) (2)
MI2 = d22 + (AB/2)2 – [2d2(AB/2)cosB] = [½ (d12 + d22)] – (¼ AB2) (thay cosB ở (2))
Thay (1) vào phương trình trên ta có: MI2 = m2 + ( ¼ k2) – (¼ AB2) = m2 + ( ¼ k2) – 10,89 (3)
Đề cho M ngoài đường tròn => d2 > 0 => m > 0,5kmax => m > 3; (4)
Và MI > AB/2 <=> MI2 > ¼ AB2 = 10,89 kết hợp với (3) ta có:
<=> m2 + (¼ k2) – 10,89 > 10,89 <=> m2 + (¼ k2) > 21,78 (5)
| m | m2 | ¼ k2 | m2 + (k2/4) > 21,78 | k |
| 4 | 16 | 0 | 16 | 0 |
| 16 | ¼ | 16,25 | 1 | |
| 16 | 1 | 17 | 2 | |
| 16 | 9/4 | 18,25 | 3 | |
| 16 | 4 | 20 | 4 | |
| 16 | 25/4 | 22,25 > 21,78 | 5: Chọn |
Vậy m = 4 và k = 5 thỏa bất đẳng thức (5) và thỏa MI nhỏ nhất;
thay m = 4 và k = 5 vào (3) ta có MI2 = 22,25 – 10,89 = 284/25 => MI = 3,37λ. Chọn A.
*** Với bài toán tương tự bài trên, nhưng M ở trong (C) và tìm MI xa nhất, cũng giải tương tự trên, tìm điều kiện cho số nguyên m, bằng cách áp dụng bất đẳng thức tam giác: d1 + d2 > AB <=> 2 m > 6,6 => m > 3,3;
Cũng dùng bảng trên để dò điều kiện: m2 + (¼ k2) < 21,78 (5′)
Ta chọn m = 4 và k = 4 thỏa (5′) và thỏa MI xa nhất, ta tính được MImax = 3,02 λ.