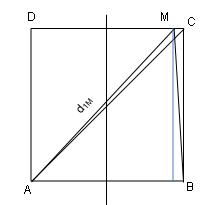
Giao thoa sóng cơ: Đỉnh hình vuông ngược pha với nguồn: Trong thí nghiệm giao thoa sóng tại mặt nước, với hai nguồn dao động theo phương thẳng đứng, cùng pha đặt tại hai điểm A và B;  ABCD là hình vuông ở mặt nước, phần tử tại C dao động ngược pha với nguồn. Trên AB có 17 điểm giao thoa cực đại. Điểm M trên CD, dao động biên độ cực đại gần C nhất và cách C là 0,4 cm. Độ dài AB gần nhất với giá trị nào sau đây?

A. 6,5 cm.                     B. 8,4 cm.                       C. 10,4 cm.                       D. 12,3 cm.

Giải: Trên AB có 17 điểm giao thoa cực đại => k_max = 8;

Giả sử: u_A = u_B = acos(ωt); Sóng từ A truyền đến C gọi là u_AC; Vì C dao động ngược pha với nguồn => u_AC ngược pha với nguồn:

u_AC = acos[ωt – (2πd_1C/λ)] => 2πd_1C/λ = q₁π với q₁ là số nguyên lẻ => d_1C = q₁λ/2           (1)

Sóng từ B truyền đến C gọi là u_BC; Vì C dao động ngược pha với nguồn => u_BC ngược pha với nguồn => u_BC cùng pha với u_AC;

u_BC = acos[ωt – (2πd_2C/λ)] => 2πd_2C / λ = q₂π với q₂ là số nguyên lẻ => d_2C = q₂λ / 2;   (2)

Ta có u_C = u_AC + u_BC = 2a. cos[π(d_1C – d_2C) / λ]. cos{ωt – [π(d_1C + d_2C) / λ]};

Vì C dao động ngược pha với nguồn nên π(d_1C + d_2C) / λ = qπ với q là số nguyên lẻ;         (3)

<=> d_1C + d_2C = qλ <=> (q₁/2) + (q₂/2) = q  (xem (1) ; (2) và (3))                                             (4)

Từ (4) ta thấy để q là số nguyên lẻ và u_AC cùng pha với u_BC nên ta chọn q₂ = q₁ + 4 hay q₂ = q₁ + 8 hay q₂ = q₁ + 12; …vì đề cho MC là nhỏ nhất nên chọn q₂ = q₁ + 4

=> q = [(q₁/2) + (q₁/2) +2] = (q₁ + 2) luôn luôn là số nguyên lẻ;

Vậy d_1C – d_2C = (q₁λ/2) – (q₂λ/2) = (q₁λ/2) – (q₁λ/2) –2 λ = -2λ => u_C = 2a. cos(2π).cos(ωt – qπ) thỏa mãn C dao động ngược pha với nguồn và C cũng là cực đại giao thoa , mà ta biết khoảng cách giữa 2 cực đại giao thoa nhỏ nhất là λ/2 => MC = λ/2 = 0,4 cm => λ = 0,8 cm;

Ta có M là cực đại giao thoa nên: d_1M – d_2M = k_Mλ với k_M = 7; 6; 5; 4; 3; 2.                              (5)

Áp dụng Pitago thay vào (5) ta có phương trình: √[d² + (d – 0,4)²] – √(d²+0,4²) = 0,8 k_M  ;    với d = AB;

Với k_M = 7; Giải pt trên ta được d = 14,21 cm => số nguyên k < d /λ => k_max = 17 => có 35 cực đại giao thoa trên AB: Loại;

Với k_M = 6; Giải pt trên ta được d = 12,28 cm => k_max = 15 => có 31 cực đại giao thoa trên AB: Loại;

Với k_M = 5; Giải pt trên ta được d = 10,35 cm => k_max = 12 => có 25 cực đại giao thoa trên AB: Loại;

Với k_M = 4; Giải pt trên ta được d = 8,42 cm => k_max = 10 => có 21 cực đại giao thoa trên AB: Loại;

Với k_M = 3; Giải pt trên ta được d = 6,49 cm => k_max = 8 => có 17 cực đại giao thoa trên AB: Thỏa đề bài

Chọn A.