- Liên hệ trung tâm
- 090 6800 598
- [email protected]
GT sóng cơ – thi TNQG 2021 lần 1 – Tất cả 4 dạng
GT sóng cơ – thi TNQG 2021 lần 1 – Tất cả 4 dạng
Đề thi TNQG 2021 lần 1 ngày 8 – 7 – 2021: mã đề 207
Giao thoa sóng cơ
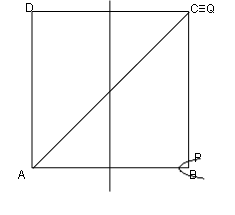
Câu 38: Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm A và B, dao động cùng pha theo phương thẳng đứng, phát ra hai sóng lan truyền trên mặt nước với bước sóng λ. Ở mặt nước, C và D là hai điểm sao cho ABCD là hình vuông. Trên cạnh BC có 6 điểm cực đại giao thoa và 7 điểm cực tiểu giao thoa, trong đó có P là điểm cực tiểu giao thoa gần B nhất và Q là điểm cực tiểu giao thoa gần C nhất. Khoảng cách xa nhất có thể giữa hai điểm P và Q là
A. 10,5λ; B. 9,96λ; C.8,93 λ; D. 8,4λ.
Giải: Ta biết để có hình ảnh giao thoa rõ nét thì AB = dλ = kλ + (λ/2) => P là cực tiểu giao thoa gần B nhất => PB ≈ λ/4; Trên BC có 6 cực đại giao thoa và 7 cực tiểu giao thoa (số cực tiểu nhiều hơn số cực đại là 1) => C là cực tiểu giao thoa => Q trùng với C;
Vậy QPmax = CP ≈ dλ – (λ/4) = (d – ¼ )λ;
Vì C là cực tiểu giao thoa nên: CA – CB = qλ (với q là số bán nguyên)
<=> d(√2 – 1)λ = qλ => q = (√2 – 1)d = 0,414 d;
Ta có: Số cực đại giao thoa trên BC thỏa mãn bất đẳng thức sau:
– |CA – CB | ≤ kλ < BA – BB <=> – (√2 – 1)d λ ≤ kλ < dλ <=> – q ≤ k < q/0,414;
Đề cho trên BC có 6 cực đại giao thoa => k = 6, thay vào bất đẳng thức trên ta được:
6 < q/0,414 => q > 2,485; Ta biết q là số bán nguyên nên chọn q = 2,5; 3,5; 4,5; 5,5; …
Lập bảng: X = q; f(X) = d = q/0,414; g(X) = f(X) – 0,25 = d – 0,25 = CP = (q/0,414) – 0,25
Với start = 2,5; end = 5,5; step = 1 ta được kết quả sau:
X = 2,5 = q; d= f(X) = 6,036; PQmax = g(X) = d – 0,25 = 5,79 : Không có đáp án;
X = 3,5 = q; d= 8,454 ; PQmax = 8,1997: sai số so với đáp án D là 2,38 %;
X = 4,5 = q; d= 10,864 ; PQmax = 10,61: sai số so với đáp án A là 1,08 % : Chọn A: 10,5λ.
Câu 38_1: (Câu 37 mã đề 214) Đồng dạng với câu trên, chỉ khác là: P là cực tiểu giao thoa gần B nhất và Q là cực đại giao thoa gần C nhất.
Giải: Giải tương tự như trên tìm ra được BC = d = 10,864λ; P là cực tiểu giao thoa gần B nhất => PB ≈ λ/4; Vì C là cực tiểu giao thoa, mà Q là cực đại giao thoa gần C nhất => Q thuộc đường hypecbol có k = 5 (vì trên AB có 21 cực đại giao thoa, kmax = 10,và trên BC có 6 cực đại giao thoa) nên ta có:
(gọi QC = x1λ) => d1Q – d2Q = 5λ <=> √[d2 + (d – x1)2] – (d – x1) = 5 (vì tất cả các độ dài có đơn vị là λ)
với d = 10,864λ ta tính được: x1 = 1,561λ
=> PQmax = BC – PB – QC = (10,864 – 0,25 – 1,561)λ = 9,05λ => Chọn Đáp án 8,93λ.
Câu 38_2: (Câu 36 mã đề 202) Đồng dạng với câu 38, chỉ khác là: P là cực đại giao thoa gần B nhất và Q là cực tiểu giao thoa gần C nhất.
Giải: Giải tương tự như câu 38 tìm ra được BC = d = 10,864λ; P là cực đại giao thoa gần B nhất => P thuộc đường hypecbol có k = 10 (vì trên AB có 21 cực đại giao thoa, kmax = 10) nên ta có:
(gọi PB = x2λ) => d1P – d2B = 10λ <=> √(d2 + x22) – x2 = 10
với d = 10,864λ ta tính được: x2 = 0,901λ
=> PQmax = BC – BP = (d – x2)λ= (10,864 – 0,901)λ = 9,963λ => Chọn Đáp án 9,96λ.
Câu 38_3: (Câu 39 mã đề 213) Đồng dạng với câu 38, chỉ khác là: P là cực đại giao thoa gần B nhất và Q là cực đại giao thoa gần C nhất.
Giải: Giải tương tự như câu 38 tìm ra được BC = d = 10,864λ; P là cực đại giao thoa gần B nhất => PB = x2 (xem 38_2); Vì Q là cực đại giao thoa gần C nhất => QC = x1 (xem 38_1)
Vậy PQmax ≈ BC – PB – QC = (d – x1 – x2)λ = (d – 1,56 – 0,901)λ = 8,402λ;
Chọn đáp án 8,4λ.