- Liên hệ trung tâm
- 090 6800 598
- [email protected]
Sóng cơ: 3 điểm thẳng hàng
Sóng cơ: 3 điểm thẳng hàng
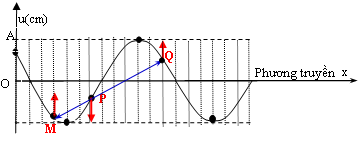
Câu II.1) Tại thời điểm t = 0, đầu O của một sợi dây đàn hồi căng ngang bắt đầu dao động theo phương vuông góc với sợi dây với tần số f = 2 Hz, sóng lan truyền trên dây với tốc độ 24 cm/s. Coi biên độ dao động của các phần tử trên dây là như nhau. Gọi M và N là hai điểm trên dây cách O lần lượt 6 cm và 9 cm. Không tính thời điểm t = 0, kể từ khi O dao động, thời điểm ba điểm O, M, N thẳng hàng lần thứ 2 là
A. 0,387 s. B. 0,463 s. C. 0,500 s. D. 0,375 s. (Đáp án: B)
(Mời các bạn giải trước khi đăng bài giải)
Giải: Ta có: λ = v/f = 12 cm; Trong hệ tọa độ Decartes: uOx, tọa độ các điểm là O(0, uO); M(6, uM) và N(9, uN);
Phương trình dao động của 3 điểm O, M và N là:
uO = Acos(ωt – π/2); uM = Acos(ωt – 3π/2) và uN = Acos(ωt – 2π);
Vì O, M, N thẳng hàng nên hệ số góc của OM và ON bằng nhau => (uM – uO)/6 = (uN – uO)/9 hay
3uM – 2uN – uO = 0 <=> 2√5 Acos(ωt + 2,03) = 0 (Dùng số phức)
=> ωt + 2,03 = ±π/2 + 2kπ => t = (1/8) – 0,162 + (0,5k) (*)
Thời điểm O, M, N thẳng hàng lần thứ 2 ứng với k = 1 thay vào (*) ta được t = 0,463 s. Chọn B.