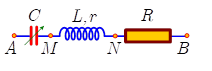
Câu 40: Đặt điện áp u = 120cos[100πt – (π/6)] vào hai đầu đoạn mạch AB mắc nối tiếp gồm: tụ điện có điện dung C thay đổi được; cuộn dây có độ tự cảm L và điện trở r; điện trở R với R = 2r như hình bên. Khi C = C₀ thì điện áp hiệu dụng giữa hai đầu đoạn mạch AN đạt cực tiểu. Khi C = C₀/4 thì điện áp hiệu dụng giữa hai đầu đoạn mạch AM đạt cực đại và điện áp giữa hai đầu đoạn mạch MN là u_MN. Biểu thức u_MN là

A. u_MN = 40cos[100πt – (2π/3) V.                      B. u_MN = 40√3cos[100πt + (π/2)] V.

C. u_MN = 40√3cos[100πt + (2π/3)] V.                D. u_MN = 40cos[100πt + (π/2)] V.

Giải:

Khi C thay đổi U_AN min khi Z_L = Z_C0

Khi C₁ = C₀/4 thì U_Cmax => u_MB ┴ u (hay tam giác M’MA vuông tại M) khi đó: Z_C1 = 4Z_C0 = 4Z_L và

Z_C1 = [(3r)² + Z_L²] /Z_L => Z_L = r√3 => Z_C1 = 4r√3 => Z₁² = (3r)² + (Z_L – Z_C1)² = 36r²

=> Z₁ = 6r => I₁ = U/(6r) = 10√2 /r => U_Cmax = Z_C1I₁ = 40√6 V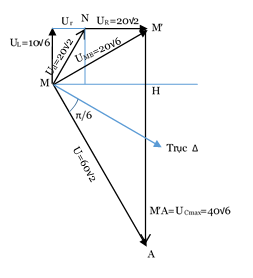

=> Theo Pitago: U_MB² = (40√6)² – (60√2)² = (20√6)² => U_MB = 20√6 V;

Áp dụng hệ thức trong tam giác vuông M’MA: (1/MH²) = (1/MM’²) + (1/MA²) => MH = U_Rr = 30√2 V => U_r = 10√2 V; Ta cũng có: MM’² = M’A. M’H => M’H = U_L = 10√6 V

=> U_MN² = U_d² = U_r² + U_L² => U_MN = 20√2 V => U_0MN = 40 V => Loại đáp án B và C;

Ta có (u_d, u) = 2π/3 = (u_d, Δ) + (Δ, u) => (u_d, Δ) = (2π/3) – (π/6) = π/2 => Chọn D.