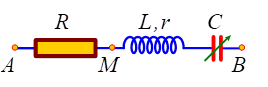
• Câu 1. (Câu 38 mã đề 221 thi THPT QG 2022) Đặt điện áp xoay chiều có giá trị hiệu dụng U = 120 V và tần số không đổi vào hai đầu đoạn mạch AB gồm điện trở R, cuộn dây có độ tự cảm L và điện trở r, tụ điện có điện dung C thay đổi được như hình bên. Khi C = C₀ hoặc C = 3C₀ thì độ lớn độ lệch pha giữa điện áp hai đầu đoạn mạch AB và điện áp hai đầu đoạn mạch MB là lớn nhất và bằng Δφ với tan Δφ = 0,75. Khi C = 1,5C₀ thì điện áp hiệu dụng giữa hai đầu R có giá trị gần nhất với giá trị nào sau đây?

 A. 38 V.                B. 112 V.                             C. 25 V.                             D. 87 V.

• Câu 2. (Câu 38 mã đề 223 thi THPT QG 2022) Đặt điện áp xoay chiều có giá trị hiệu dụng U và tần số không đổi vào hai đầu đoạn mạch AB gồm điện trở R, cuộn dây có độ tự cảm L và điện trở r, tụ điện có điện dung C thay đổi được như hình bên. Khi C = C₀ hoặc C = 3C₀ thì độ lớn độ lệch pha giữa điện áp hai đầu đoạn mạch AB và điện áp hai đầu đoạn mạch MB là lớn nhất và bằng Δφ với tan Δφ = 0,75. Khi C = 1,5C₀ thì điện áp hiệu dụng giữa hai đầu R có giá trị là 67,5V. Giá trị của U gần nhất với giá trị nào sau đây?

 A. 103 V.                B. 192 V.                         C. 86 V.                             D. 205 V.

GIẢI:

Câu 1. Ta có Δφ = (u_AB, u_MB) = (u_AB, i) + (i, u_MB) = (u_AB, i) – (u_MB, i) = j – j_MB ;

Ta có tan j = (Z_L – Z_C) /R ; tan j_MB = (Z_L – Z_C) /r ;

tan Δφ = (tan j – tan j_MB) / [1 + (tan j . tan j_MB)] = R(Z_C – Z_L) / [(R + r)r + (Z_L – Z_C)²]

= R / [((R + r) r /(Z_L – Z_C)) + (Z_L – Z_C)]

Để tan Δφ max (ứng với Δφ max) thì mẫu số phải min, áp dụng bất đẳng thức Cauchy cho mẫu ta có: ((R + r) r /(Z_L – Z_C)) + (Z_L – Z_C) min khi ((R + r) r /(Z_L – Z_C)) = (Z_L – Z_C)

<=> (Z_L – Z_C)² = (R + r) r                                                       (1)

=> tan Δφ = R / [2√((R + r) r)] = 0,75 => R = 3r                   (2)

Khi C = C₀ từ (1) => Z_C0 – Z_L = √[(R + r)r]                           (3)

Khi C = 3C₀ từ (1) => Z_L – (Z_C0 /3) = √[(R + r)r]                  (4)

Từ (2), (3) và (4) => Z_C0 = 1,5Z_L ;

Khi C = 1,5C₀ => Z_C = Z_C0 / 1,5  = 1,5Z_L / 1,5 = Z_L : có cộng hưởng điện => U_Rr = 120 V

Hay U_R + U_r = 120 V = U_R + (U_R/3) = 120 V (xem (2))

=> U_R = 90 V. Chọn D.

Câu 2. Giải như trên ta có :

Khi C = 1,5C₀ => Z_C = Z_C0 / 1,5  = 1,5Z_L / 1,5 = Z_L : có cộng hưởng điện => U_Rr = U

Hay U_R + U_r = U <=> U_R + (U_R/3) = U (xem (2))

=> U = 90 V. Chọn C.