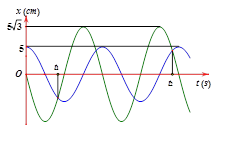
Hai chất điểm dao động điều hòa cùng tần số trên hai đường thẳng song song kề nhau, cách nhau 5 cm và song song với trục Ox có đồ thị li độ như hình vẽ. Vị trí cân bằng của hai chất điềm đều ở trên một đường thẳng qua gốc tọa độ và vuông góc với Ox. Nếu t₂ – t₁ = 1,08 s thì kể từ lúc t = 0, thời điểm hai chất điểm cách nhau một khoảng 5 √3 cm lần thứ 2016 là

1. A. 9057/25 s                             B.   9063/25 s                             C. 12091/12 s                            D. 725,6 s

Từ hình vẽ ta thu được phương trình dao động của hai chất điểm:

x1 = 5 cos(ωt);  x2 = 5√3 cos(ωt +0,5π);

với T = 1,08/1,5 = 0,72 s;

O₁O₂ = 5 cm;

lúc t = 0 thì M₁(0) = 5 cm ở A₁; M₂(0) ở O₂;

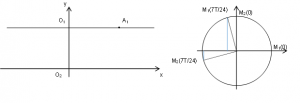
Chọn hệ trục Decartes: xO₂y ta có tọa độ của chất điểm 1  và 2 lần lượt là (x₁, 5) và (x₂, 0);

Khoảng cách giữa 2 chất điểm trong hệ xO₂y là:

D² = (x₁ – x₂)² + (y₁ – y₂)² ⇔ 75 = (x₁ – x₂)² + 5²                (*)

=> |x₁ – x₂| = √2

⇔ |cos(ωt) – [√3 cos(ωt + (π/2))] | = √2

⇔ |cos(π/3)cos(ωt) + sin(π/3)sin(ωt) | = √2cos(π/3)

=> cos(ωt – π/3) = cos(π/4) (xét trong góc phần tư thứ nhất)

=> t = 7π/(12ω) = 7T/24 là thời điểm đầu tiên 2 chất điểm cách nhau 5√3 cm;

Ta có: x₁(7T/24) = -1,294 cm;

x₂(7T/24) = -8,365 cm,

Sử dụng số phức ta có: x₁ – x₂ = 10 cos(ωt – π/3) kết hợp với (*) => cos(ωt – π/3) = √2/2

ta thấy trong 1 chu kỳ (trên 1 vòng tròn) có 4 thời điểm cách đều nhau T/4, mà khoảng cách 2 chất điểm là 5√3 cm;

Ta có :  2016/4 = 504 chu kỳ, vậy sau 504 chu kỳ là lần thứ 2017 hai chất điểm có khoảng cách là 5√3 cm, vậy thời gian cần tìm là :

t = (7T/24) + 504T – (T/4) = 362,91 s. Chọn B.