- Liên hệ trung tâm
- 090 6800 598
- [email protected]
Lò xo – Thi TN QG 2023
Lò xo – Thi TN QG 2023
Thi TN QG 29/6/2023
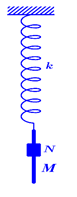
Câu 38 (Mã đề 221, câu 36 mã đề 203): Một con lắc lò xo treo thẳng đứng gồm lò xo nhẹ có độ cứng k = 100 N/m và vật M khối lượng 100 g có dạng một thanh trụ dài. Vật N được lồng bên ngoài vật M như hình bên. Nâng hai vật lên đến vị trí lò xo không biến dạng rồi thả N để N trượt thẳng đứng xuống dọc theo M, sau đó thả nhẹ M. Sau khi thả M một khoảng thời gian 1/15 s thì N rời khỏi M . Biết rằng trước khi rời khỏi M thì N luôn trượt xuống so với M và lực ma sát giữa chúng có độ lớn không đổi và bằng 1 N. Bỏ qua lực cản của không khí. Lấy g = 10 m/s2 và π2 = 10. Sau khi N rời khỏi M, M dao động điều hòa, độ biến dạng cực đại của lò xo là Δlmax. Giá trị Δlmax gần nhất với giá trị nào sau đây?
A. 4,1 cm. B. 3,6 cm. C. 3,1 cm. D. 4,6 cm.
Giải:
Lực ma sát tác dụng lên M có hướng xuống, vị trí cân bằng của M khi có ma sát là O’ với
OO’ = Fms / k = 0,01 m = 1 cm ; Khi t = 0 thì M ở biên âm với biên độ:
A(O’ ) = Δl0 + OO’ = (Mg/k) + 1 = 2 cm ; Chu kỳ T = 2π√(M / k) = 0,2 s => w = 10π rad/s ;
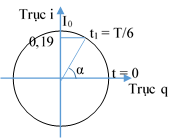
Δt = 1/ 15 s = T/3 => x(Δt)(O’ ) = A(O’ ) / 2 = 2 / 2 = 1 cm (xem vòng tròn)
=> x0 = OO’ + x(Δt)(O’ ) = 1 + 1 = 2 cm là ly độ của vị trí N rời đi so với O ;
Vận tốc của M khi N rời đi là: v(Δt) = vmax√3 /2 = A(O’ )w√3 /2 = 2w√3 /2 = w√3 cm/s ;
Biên độ của M khi N rời đi: A(O) = √[x02 + (v(Δt) / w)2] = √[ 22 + 3] = √7 cm = 2,64 cm ;
Vậy Δlmax = Δl0 + A(O) = 1 + 2,64 = 3,64 cm. Chọn B.