Đề thi TNQG 2021 lần 1 ngày 8 – 7 – 2021 ; mã đề 207

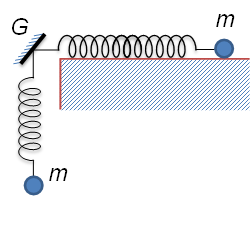
Câu 40:  Hai con lắc lò xo giống hệt nhau được gắn vào điểm G của một giá cố định như hình bên. Trên phương nằm ngang và phương thẳng đứng, các con lắc đang dao động điều hòa cùng biên độ 14 cm, cùng chu kì T nhưng vuông pha với nhau. Gọi F_G là độ lớn hợp lực của các lực do hai lò xo tác dụng lên giá. Biết khoảng thời gian ngắn nhất giữa hai lần mà F_G bằng trọng lượng của vật nhỏ của mỗi con lắc là T/4. Lấy Giá trị của T gần nhất với giá trị nào sau đây?

A. 0,58 s.                     B. 0,62 s.                              C. 0,74 s.                           D. 0,69 s.

Giải: Khi con lắc ngang tác dụng lực đàn hồi lên G có độ lớn cực đại bằng kA, thì con lắc dọc tác dụng lực đàn hồi lên G có độ lớn bằng 0 (vì 2 con lắc dao động vuông pha); Khi con lắc ngang tác dụng lực đàn hồi lên G có độ lớn bằng 0 thì con lắc dọc tác dụng lực đàn hồi lên G có độ lớn cực đại bằng (kA + k∆l₀); Vậy độ lớn của F_G nằm trong khoảng [kA; kA+ k∆l₀].

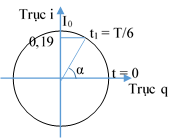
Đoạn thẳng HV là quỹ tích của điểm ngọn của vector F_G; Khi F_G có vị trí như hình vẽ (dựa vào dữ kiện T/4, ta suy ra góc 45⁰), thì độ lớn của nó bằng trọng lượng của vật m: F_G = k.∆l₀ = d₂;

Ta có: d₄² = d₁² + d₂² – d₁d₂√2;                        với d₁ = kA; d₃ = kA + (k.∆l₀);

Và d₅² = d₃² + d₂² – d₃d₂√2;                  Theo Pitagor ta có:

(d₄ + d₅)² = d₁² + d₃² <=> d₄² + d₅² + 2d₄d₅ = (kA)² + [kA + (k.∆l₀)]²;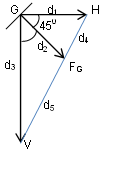

Thay d₄ và d₅ vào phương trình trên, sau khi biến đổi và rút gọn ta được:

∆l₀[(2A√2) – (2 – √2)∆l₀] = 2√{[∆l₀² + A² – (A.∆l₀√2)] [(2 – √2)∆l₀² + A² + ((2 – √2)A.∆l₀)]}

<=> ∆l₀[(2A√2) – (2 – √2)∆l₀] = 2√{[(2 – √2)∆l₀⁴] + A⁴ + [(4 – 3√2)A.∆l₀³] + [(2 – 2√2)A³∆l₀] + [(5 –3√2)A²∆l₀²]}

Bình phương 2 vế phương trình trên để mất dấu căn, thay A = 14 cm, sau khi biến đổi và rút gọn ta được:

– 2X⁴ + (56√2 – 112)X³ + [(28√2)² – 4(5 – 3√2).14²]X² – [4(2 – 2√2).14³X] – [14⁴. 4] = 0 với X = ∆l₀;

<=>-2X⁴ + (56√2 – 112)X³ + [974,230299]X² + [9092,816121]X – [14⁴.4] = 0

Dùng Shift – Solve giải được: X = 13,04592888 cm => ω² = g /X = 76,65 => ω = 8,76 rad/s => T = 2π/ω = 0,72 s. Chọn C.

Nhận xét: Do 2 lò xo dao động nên tam giác HGV quay tròn đều; Cách giải này thỏa mãn điều kiện F_G có độ lớn bằng mg và thỏa điều kiện “khoảng thời gian ngắn nhất giữa hai lần mà F_G bằng trọng lượng của vật nhỏ của mỗi con lắc là T/4”, trong khi đó cách giải ra T = 0,62 s chưa chắc đảm bảo điều kiện này.

Cách giải ra 0,62 s như sau: (các cách sau đều có chỗ áp đặt không rõ ràng, rất khó hiểu) Cách 1:

Cách 2:

Giả sử: x_d = Acos(ωt) là ly độ của lò xo treo dọc;

x_n = Acos(ωt + π/2) là ly độ của lò xo ngang;

Ta có: F_{đh_n} = F_kv = ma = – mω²x_n = – kx_n = – kAcos(ωt + π/2) = kAcos(ωt + 3π/2);      (1)

F_{đh_d} = – k. Δl = – k(Δl₀ + x_d) = – kΔl₀ –  kx_d = – kΔl₀ – kAcos(ωt) = – kΔl₀ + kAcos(ωt + π) ;          (2)

Hai lực trên có phương vuông góc với nhau nên: F_G² = (F_{đh_n})² + (F_{đh_d})² ;

Đề cho F_G = mg = kΔl₀ thay vào trên, kết hợp với (1) và (2); Sau những biến đổi, rút gọn, ta có:

0 = A² – [2Acos(ωt + π).Δl₀]  với cos(ωt + π) = π/4 (chỗ này cũng áp đặt)

=> Δl₀ = A/√2 = 9,9 cm;

Ta có ω² = g/ Δl₀ = 10,052 => ω = 10,05 rad/s => T = 0,635 s. Chọn đáp án 0,62 s.